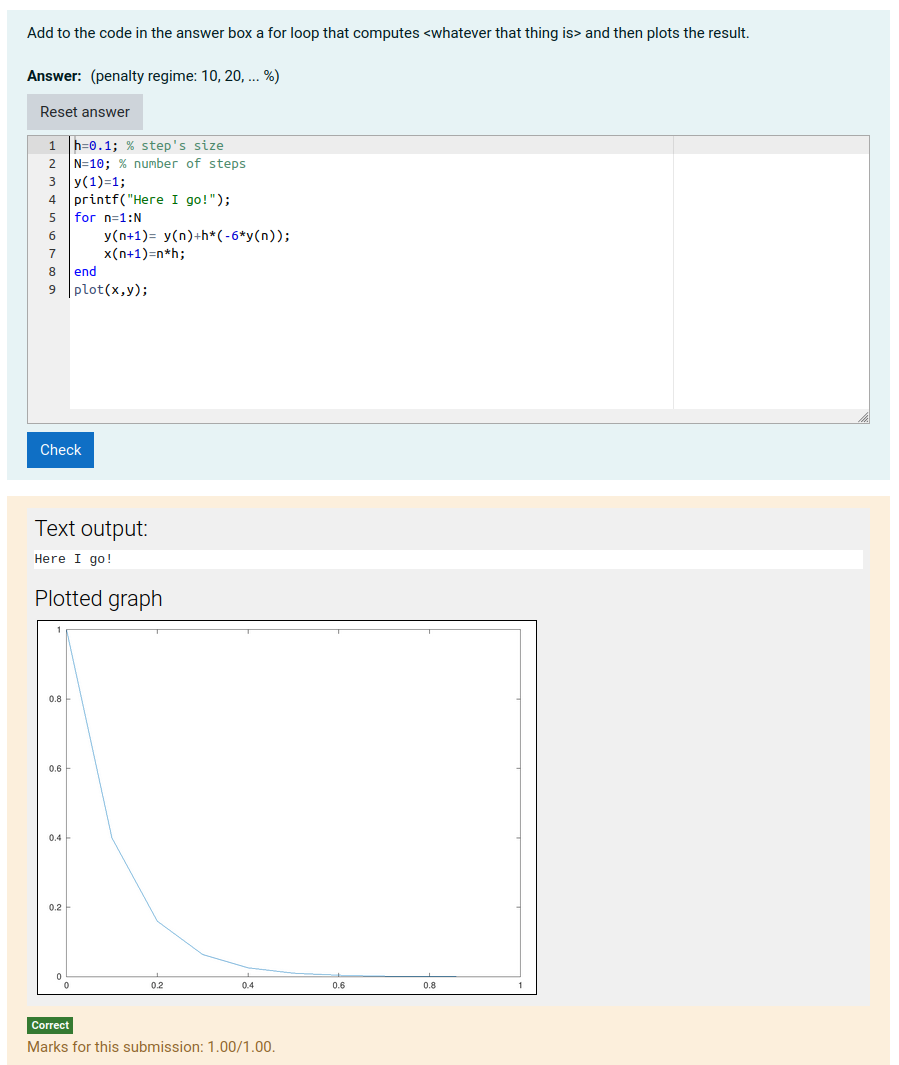
Yes, I think asking students to print the values they compute is much easier than trying to display a graph and then grade it. Here, for example, is a question from our introductory programming course for engineers:
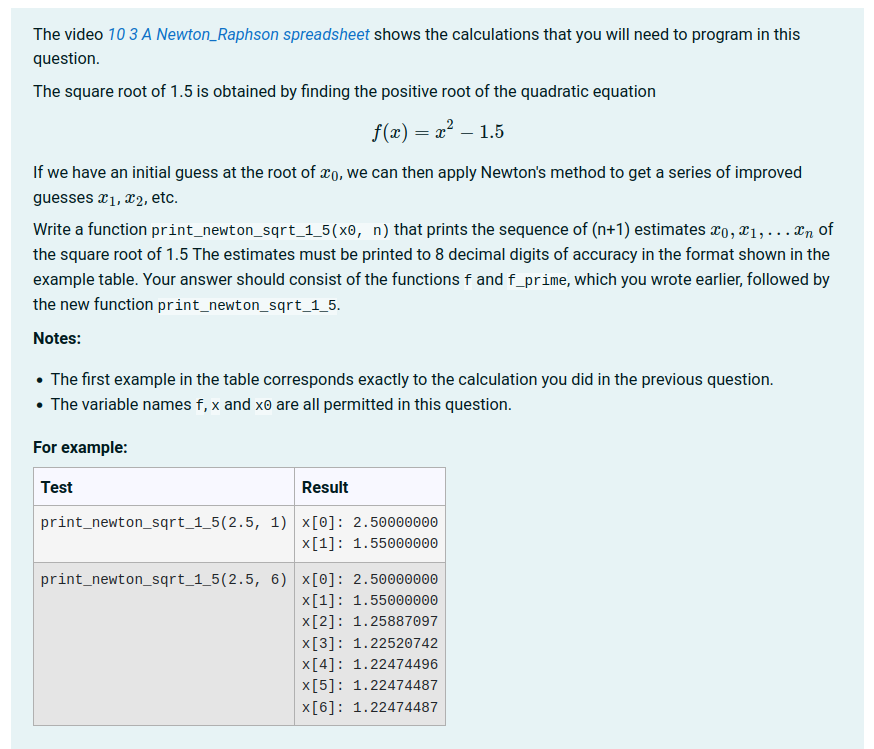
However, you do need to be very careful to deal with numerical rounding errors with questions of this sort. The grader we use in questions of this sort parses both the expected output and the student output for floating point numbers, and then compares these to within an acceptable tolerance. This is again advanced question authoring. A much simpler approach is to get the student to write a function that returns an array of expected values, then the test case you write can loop through the values, comparing with the expected one to within a given tolerance.
You can compute the expected results in a bit of code in the Extra field of the testcase and use a template that runs the code in the Extra field immediately before the code in the Test field. For example, the template might be the following (the same as the Octave function template with on extra line):
{{ STUDENT_ANSWER }}
format free
{% for TEST in TESTCASES %}
{{ TEST.extra }}; % This is the new line I added
{{ TEST.testcode }};
{% if not loop.last %}
disp('##');
{% endif %}
{% endfor %}
@17943918#@>
Then you have might an Extra field in a test like
for i = 1:10
expected(i) = ... ; % Whatever
endfor
And a test like
got = student_func(param1, param2, ...);
% Now we check your answer against our hidden expected one
for i = 1:10
if (abs(got(i) - expected(i)) > 1.e-5)
printf("Wrong answer for got(%d): expected %.5f, got %.5f\n", i, got(i), expected(i)")
endif
endfor
There are probably lots of errors in there - my octave is rusty. But hopefully the general idea is clear.